1577. So you want to be a 2^n-aire?
The player starts with $1 and
must consecutively answer n questions. Before each question, the player
can:
·
stop
the game and take the money currently in hand;
·
answer
the question. If the answer is incorrect, the player leaves the game with
nothing. If the answer is correct, the amount of money doubles, and the game
proceeds to the next question.
After correctly answering the last
question, the player keeps the winnings. The player’s goal is to maximize the
expected amount of money won.
For each individual question, the player
answers correctly with probability p. Assume that p is uniformly
distributed over the interval [t; 1].
Input. Each line represents a separate test case and
contains two numbers: an integer n (1 ≤ n ≤ 30) and a real number t (0 ≤ t
≤ 1). The last line
contains two zeros and should not be processed.
Output. For each test case, print on a separate line the
maximum expected amount of money the player can win under the optimal strategy.
Print the answer with three decimal digits.
|
Sample
input |
Sample
output |
|
1 0.5 1 0.3 2 0.6 24 0.25 0 0 |
1.500 1.357 2.560 230.138 |
SOLUTION
probability theory
Algorithm analysis
Let f(n, a)
be the maximum possible expected winnings if the player has to answer n questions
and the initial amount is a.
If n = 0, the player keeps the
initial amount, that is, f(0, a) = a.
The probability of
answering a question correctly is p, where t £ p £ 1. If the player answers the first
question correctly, there remain n – 1 questions, and the prize doubles to 2a. With probability 1 – p, the player gives an
incorrect answer and loses everything. Therefore, the expected winnings
after the first question is
p * f(n –
1, 2a) + (1 – p) * 0 = p * f(n – 1, 2a)
If this value exceeds the
current amount a, it is advantageous to continue the game; otherwise, the
player should stop. Thus, the expected winnings after making the decision to
continue is
max(a, p * f(n – 1,
2a))
Since the probability p is uniformly distributed over the
interval [t; 1],
then
f(n, a)
= 
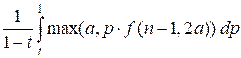
If t = 1, then the probability of a
correct answer equals one, and the player should answer all n questions,
obtaining a final prize of 2n.
Example
Let us consider the third
test, where n = 2, t = 0.6. The initial amount is a = 1.
f(2, 1) = 
,
f(1, 2) = 
,
f(0, 4) = 4
Let us compute the value
of
f(1, 2) using f(0, 4):
f(1, 2) = = 
=
/ taking into account that 4p >
2 for 0.6 £ p £ 1 /
= 
=
5 * (1 – 0.36) =
5 * 0.64 = 3.2
Let us compute the value
of f(2, 1) using f(1, 2):
f(2, 1) = 
= 
=
/ taking into account that 3.2p
> 1 for 0.6 £ p £ 1 /
= 
=
4 * (1 – 0.36) =
4 * 0.64 = 2.56
Algorithm implementation
The function integral
computes the value of the integral
I(a, k)
= 
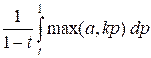
for given real numbers a and k. When t = 1, the guessing probability p equals one, so the value
of the integral I(a, k) is set to max(a, k).
Below is the region whose
area corresponds to the value of the integral 
:
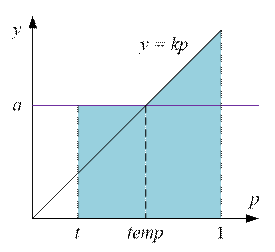
Let us find the intersection point of the lines y = a and y = kp:
a = kp, hence p = a/k
Let temp = a / k. We consider the value of the integral
as the sum of two parts: 
+ 
. Depending on the position of the point temp relative to t and 1, we
compute the value of the integral I(a,
k).
·
If t £ temp £ 1, then + =
a * (temp – t) + k * (1 – temp * temp) / 2
·
If temp £ t, then + = 
= k * (1 – t * t) / 2.
·
If temp > 1, then + = 
= a * (1 – t).
double integral(double
a, double k)
{
double s = 0,
temp = a / k;
if (t == 1) return max(a,k);
if (temp >
1) return a * (1 - t);
if (temp
>= t) s = a * (temp - t);
else temp =
t;
s += k * (1 – temp * temp) / 2;
return s / (1
- t);
}
The function f
recursively computes the value of
f(n, a) =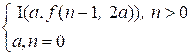 
double f(int
n, int a)
{
if (!n) return a;
double k =
f(n-1,2*a);
return
integral(a,k);
}
The main part of the
program. Read the input data, and print the value of f(n, 1).
while(scanf("%d
%lf",&n,&t),n + t)
printf("%.3lf\n",f(n,1));